ENGINEERING TRANSACTIONS
ROZPRAWY INŻYNIERSKIE
A QUARTERLY JOURNAL
- A. Ziółkowski:
Simple shear test in identification of constitutive behaviour of
materials submitted to large deformations - hyperelastic materials caseF
- Y. Liu, A.D. Foster, J. Lin, D.C.J. Farrugia, T.A. Dean:
On micro-damage in hot metal working. Part 1: Experimental investigation
- W. Dornowski, P. Perzyna:
Investigation of macrocrack propagation along a bimaterial interface in adiabatic dynamic
processes as a problem of mesomechanics
- A. Rehman, A. Khan, A. Ali:
Rayleigh waves speed in transversely isotropic material
- K. Cabańska-Płaczkiewicz:
Vibrations of the three-layer shell with damping
- A. Ziółkowski:
Simple shear test in identification of constitutive behaviour of materials submitted
to large deformations - hyperelastic materials caseF
- The present work is directed at evaluation of the simple shear test for identification of constitutive
behaviour of materials submitted to large deformations. For that purpose, actual experimental conditions
together with theoretical background of the test are analyzed on the example of two hyperelastic material
models. Advantages and disadvantages of various strain and stress measures used for presentation of simple
shear test (SST) results are analyzed. The most often presented as the only result of "standard" SST proof
chart, i.e. shear nominal stress ↔ shear nominal strain (σ12(N) ↔
γ/2), characterizes the material energetically in the sense that it reveals its capacity for
elastic energy storage dW/V0 = σ12(N) dγ. However,
it characterizes the constitutive behaviour of the material only partially, since it is equivalent to shear
II Piola Krichoff stress ↔ shear Green-Lagrange strain (σ21(2) ↔
E21(2)) chart, within the large deformations context. This data alone does not
even allow to reconstruct the shear Cauchy stress ↔ shear spatial Hencky strain
(σ12(0) ↔ e12(0)) chart for the tested
material. In order to take full advantage of the constitutive information available from simple shear test,
it is highly recommended to extend the experimental methodology of "standard" SST proof in such a way as
to determine simultaneously two components (shear and normal) of nominal stress tensor in the same SST
proof. Such experimental information allows for subsequent recalculation of non-symmetric nominal stress
tensor components into Cauchy stress components.
Contents
- Y. Liu, A.D.Foster, J. Lin, D.C.J. Farrugia, T.A. Dean:
On micro-damage in hot metal working. Part 1: Experimental investigation
- An experimental programme was defined and performed to investigate the characteristics of micro-damage
for a plain CMn and a free machining steel under hot forming conditions. To investigate damage locations -
at grain boundaries and around second phase inclusions - a series of constant strain rate tests were carried
out on the free machining steel, which contained manganese sulphide inclusions. Specimens from both materials
were strained to failure under tension using a Gleeble material simulator at a constant temperature of
1273 K, with strain rates
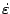= 0.01-10 s-1. The damage characteristics of the two different
steel microstructures was analysed through microstructural examinations of the tested specimens. Particular
attention is focussed on damage locations and features. To investigate the recovery of materials between the
intervals of hot deformation, a series of two-step tensile tests were carried out at 1273 K and
10 s-1. The two-step specimens were initially deformed to a strain varying from 0.3-0.7,
held for varying recovery periods of 0.3-10 s, then stretched to failure. Flow stress features and
strains to failure during the second stage of deformation were analysed with respect to different recovery
periods and strain levels at the first stage of deformation. The damage features discovered from the
experimentation and microstructural examination provide theoretical evidence to form unified viscoplastic
damage constitutive equations for hot forming of free machining steels, which are described in the companion paper.
Contents
- W. Dornowski, P. Perzyna:
Investigation of macrocrack propagation along a bimaterial interface in adiabatic dynamic
processes as a problem of mesomechanics
- The main objective of the present paper is the investigation of macrocrack propagation along
a bimaterial interface in adiabatic dynamic processes. The investigation has been generated by very
recent experimental observation (cf. Rosakis, Samudrala and Coker [34], Guduru, Rosakis and Ravichandran
[13], Guduru, Zehnder, Rosakis and Ravichandran [14]).
- A general constitutive model of elastic-viscoplastic damaged polycrystalline solids has been developed
within the thermodynamic framework of the rate-type covariance material structure with a finite set of
internal state variables. This set of internal state variables will be assumed and interpreted so that
the theory developed has been taken into account the effects as follows: (i) plastic non-normality;
(ii) softening generated by microdamage mechanisms; (iii) thermomechanical coupling (thermal plastic
softening and thermal expansion); (iv) strain-rate sensitivity. It is noteworthy to stress that viscosity
introduces implicitly a length-scale parameter into the dynamical initial boundary value problem.
- In order to describe in a constitutive model all the previously mentioned properties and incorporate
their respective effects, it is intended to introduce a particular set of internal state variables, which
consists of the equivalent inelastic deformation and volume fraction porosity. The equivalent inelastic
deformation can describe the dissipation effects generated by viscoplastic flow phenomena and the volume
fraction porosity takes into account the microdamage evolution effects. The kinetics of microdamage plays
a very important role in this constitutive model. Fracture criterion based on the evolution of microdamage
is assumed. The relaxation time is viewed either as a microstructural parameter to be determined from
experimental observations, or as a mathematical regularization parameter. By assuming that the relaxation
time tends to zero, the rate-independent elastic-plastic response can be obtained. The identification
procedure is developed basing on the experimental observations.
- We consider isothermal and adiabatic processes in the thin flat specimen made of two identical elements
(material A) and the cohesive band (material B). The width of the cohesive band is 1 μm, so it is a
mesoscale size range. In this cohesive band the initial notch is localized symmetrically. It is assumed that
the boundary conditions are modelled by the speed of the upper edge of the specimen, while the lower edge
is clamped. The initial conditions of the problem are homogeneous. Both materials of the specimen are
modelled as elastic-viscoplastic.
- A two-dimensional, plane stress, finite-difference model of the entire specimen is applied. The numerical
algorithm satisfies the material objectivity, i.e. is invariant with respect to any diffeomorphism (any motion).
- Particular attention is focused on the investigation of interaction of stress waves on the propagation of
macrocrack within the interface band. The macrocrack-tip speed history and the evolution of the transient
macrocrack-tip temperature fields are obtained.
Contents
- A. Rehman, A. Khan, A. Ali:
Rayleigh waves speed in transversely isotropic material
- Rayleigh wave speed in transversely isotropic material is studied. A very simple technique is adopted
to solve the secular equation. Speed in some transversely isotropic materials is calculated.
Contents
- K. Cabańska-Płaczkiewicz:
Vibrations of the three-layer shell with damping
- In this paper the analytical method [17, 18] has been used for solving the problem of vibrations of
the three-layer shell with damping. External layers are modelled as the MINDLIN shells and the internal
layer possesses the characteristics of a viscoelastic one-directional WINKLER foundation. Small transverse
vibrations of the three-layer shell with damping is excited by the dynamical non-uniform loading moving at
the constant velocity v*. Numerical results are presented in the diagrams.
Contents
Reprints of the full papers may be obtained from their authors.
Contact Editorial Office in case you need
the address of the respective author.
Previous issue
